C program to convert decimal to hexadecimal number

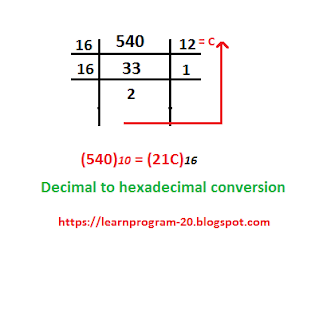
Decimal to hexadecimal conversion

In this section, we can convert any decimal number(base 10) into hexadecimal number (base 16) by c program and with example.

Hexadecimal range: 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F

Example: Program to convert Decimal to hexadecimal

#include<stdio.h>

int main()

{

    int decnum, rem, i=0;

    char hexnum[50];

    printf("Enter any decimal number: ");

    scanf("%d", &decnum);

    while(decnum!=0)

    {

        rem = decnum%16;

        if(rem<10)

            rem = rem+48;

        else

            rem = rem+55;

        hexnum[i] = rem;

        i++;

        decnum = decnum/16;

    }

    printf("\nEquivalent Value in Hexadecimal = ");

    for(i=i-1; i>=0; i--)

        printf("%c", hexnum[i]);

    

    return 0;

}

Output :

Enter any decimal number: 2020

Equivalent Value in Hexadecimal = 7E4

PRACTICE PROBLEMS BASED ON DECIMAL TO HEXADECIMAL CONVERSION-

 

Convert the following numbers from base 10 to base 16-

1. (2020)₁₀
2. (2020.65625)₁₀

 

Solution-

 

1. (2020)₁₀

 

(2020)₁₀ → (?)₁₆

 

Using division method, we have-

 

 

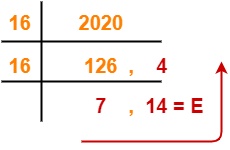
From here, (2020)₁₀ = (7E4)₁₆

 

2. (2020.65625)₁₀

 

(2020.65625)₁₀ → ( ? )₈

 

Here, we treat the real part and fractional part separately-

 

For Real Part-

 

• The real part is (2020)₁₀
• We convert the real part from base 10 to base 16 using division method same as above.

 

So, (2020)₁₀ = (7E4)₁₆

 

For Fractional Part-

 

• The fractional part is (0.65625)₁₀
• We convert the fractional part from base 10 to base 16 using multiplication method.

 

Using multiplication method, we have-

 

Explanation   Step-01:   Multiply 0.65625 with 16. Result = 10.5. Write 10 (= A in hexadecimal) in real part and 0.5 in fractional part.   Step-02:   Multiply 0.5 with 16. Result = 8.0. Write 8 in real part and 0.0 in fractional part.   Since fractional part becomes 0, so we stop.

 

 

• The fractional part terminates to 0 after 2 iterations.
• Traverse the real part column from top to bottom to obtain the required number in base 16.

 

From here, (0.65625)₁₀ = (0.A8)₈

 

Combining the result of real and fractional parts, we have-

(2020.65625)₁₀ = (7E4.A8)₁₆